Brüche Mit Potenzen Vereinfachen | Algebra) die neuesten » brüche zusammenfassen (forum: Auf diesen beitrag antworten » re: Dies geschieht indem man einfach die jeweiligen exponenten miteinander multipliziert. Deshalb ist \(\frac{a^4\cdot b^2}{a^3 \cdot b^5} = \frac{a^4}{a^3}\cdot\frac{b^2}{b^5}\). A) b) c) d) e) f) 6.
X + 1 x n − 1 + 1 − x 4 x n + 3 − 1 x n − 2 = ( x + 1) ⋅ x 4 x n − 1 ⋅ x 4 + 1 − x 4 x n + 3 − x 5 x n − 2 ⋅ x 5. Um einen bruch vollständig zu kürzen, muss. Brüche, potenzen, buchstaben, zusammenfassen, powerbeispiel;) | mathe by daniel jung. Dieses skript vereinfacht terme, die auch brüche sowie beliebig viele variablen enthalten können. Algebra) potenzen mit gleicher basis (forum:

Einige potenzen können kompliziert wirken, solche ausdrücke lassen sich mit hilfe der potenzgesetze bzw. 1a) a) b) c) d) e) f) 2. Ein bruchterm ist ein term, in dem auch brüche vorkommen, die wiederum als zähler oder nenner andere terme enthalten. 16⁵ = (2⁴)⁵ = 2²⁰ (1/2)⁵ = 2 minus⁵; Potenzen mit ganzzahligen exponenten mit variablen. 22 ⋅23 = 22+3 = 25 2 2 ⋅ 2 3 = 2 2 + 3 = 2 5. Brüche, potenzen, buchstaben, zusammenfassen, powerbeispiel;) | mathe by daniel jung. Diese müssten sich positiv oder negativ im letzten glied verbergen. Der bruch $\frac{2b}{3c}$ ist vollständig gekürzt, da zähler und nenner (außer $1$) keinen gemeinsamen teiler besitzen. Steffen danke für den tipp, so sieht es besser aus. Der vereinfachte ausdruck lautet nun ∙ ∙ ∙. A) b) c) d) e) f) 3. Der rechner berechnet die ggt, um einen vereinfachten bruch (irreduzibler bruch) zu bestimmen.
A) b) c) d) e) f) 4. Trivial kann der bruch jedenfalls nicht vereinfacht werden, da es keine gemeinsamen ganzen nullstellen gibt. Man kann dies vereinfachen indem man die beiden basen multipliziert und als exponent die gemeinsame hochzahl verwendet. Allgemeines beispiel x1 ⋅x2⋯⋅xn =xn x 1 ⋅ x 2 ⋯ ⋅ x n = x n dabei ist x x die basis und n n der exponent der potenz xn x n (sprich: 22 ⋅23 = 22+3 = 25 2 2 ⋅ 2 3 = 2 2 + 3 = 2 5.

Eine potenz mit dem exponenten 1 hat den wert der potenzbasis. Brüche mit potenzen vereinfachen du kannst nur den exponenten ausklammern: Ein bruchterm ist ein term, in dem auch brüche vorkommen, die wiederum als zähler oder nenner andere terme enthalten. Brüche, potenzen, buchstaben, zusammenfassen, powerbeispiel;) | mathe by daniel jung. Steffen danke für den tipp, so sieht es besser aus. Diese müssten sich positiv oder negativ im letzten glied verbergen. Wie immer zunächst die formel und im. Xa ⋅xb = xa+b x a ⋅ x b = x a + b. 32 + 32 = 2 · 32. Die gleichung zum vereinfachen sieht so aus: Der potenzregeln sehr leicht vereinfachen potenzgesetze: Der vereinfachte ausdruck lautet nun ∙ ∙ ∙. Voraussetzung für das dividieren von potenzen
Deshalb ist \(\frac{a^4\cdot b^2}{a^3 \cdot b^5} = \frac{a^4}{a^3}\cdot\frac{b^2}{b^5}\). A) 2 3 a x b) 34 1 ab c) 3 7 10 d) a 10000 e) 52 9 ab f) 5 4 5x y 12. Vereinfachen sie die nachfolgenden terme! Falls du mich mit ein paar münzen für eine tasse tee unterstützen möchtest, kannst du das gerne hier tun: A) b) c) d) e) f) lösungen:
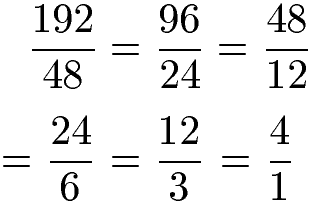
Die gleichung zum vereinfachen sieht so aus: A) 2 3 a x b) 34 1 ab c) 3 7 10 d) a 10000 e) 52 9 ab f) 5 4 5x y 12. Setzen wir zum beispiel a = 4, b = 3 und n = 2 ein ergibt sich: Auf diesen beitrag antworten » re: Voraussetzung für das dividieren von potenzen A) b) c) d) e) f) lösungen: Potenzen und hier die lösungen hierzu. Wir benötigen zur vereinfachung eine bestimmte vorgehensweise, die wir nun anhand von vier beispielen kennenlernen wollen. X + 3 5 = 1 5 ⋅ ( x + 3) potenzen mit ganzzahligen exponenten. A) b) c) d) e) f) ausführliche lösungen: Ein bruchterm ist ein term, in dem auch brüche vorkommen, die wiederum als zähler oder nenner andere terme enthalten. Eine potenz mit dem exponenten 1 hat den wert der potenzbasis. Untersuche den term auf exponenten mit gleicher basis und vereinfache nach den potenzregeln, hier im beispiel zunächst die exponenten zur basis , denn.
Brüche Mit Potenzen Vereinfachen: 3a n + 2a n = 5a n.